LLM optimizations for sparse matrix processing on Jetson Orin and other Ampere GPUs

While the advent of Large Language Models has brought significant leaps in many areas including text analysis and computer vision, translating to benefits across a variety of industries, the size of the models can be a limitation to their usability. As LLMs often require several dozen gigabytes of RAM, optimizing models for accuracy and performance, e.g. for small footprint edge AI setups, is a very pressing issue.

Architectures since NVIDIA’s Ampere used in many recent GPUs and eGPUs (including the Jetson Orin series SoMs), offer instructions for Tensor Cores capable of operations on sparse matrices, enabling previously unattainable model optimization potential on low-precision (8-bit, 4-bit per value) sparse tensors. To tap into these possibilities and expand the capabilities of our open source Kenning framework, Antmicro developed open source CUDA-accelerated kernels which leverage optimizations performed by two open source algorithms – the recently popular GPTQ for quantization and SparseGPT for pruning.

In this article, we go over how the new addition to Antmicro’s end-to-end AI application optimization and deployment toolkit utilizes the new instructions available in CUDA’s ISA and how these optimizations let us adjust such substantial models for lower resource consumption and better performance, especially in size constrained use cases like space-bound AI-enabled devices. We also present metrics of potential improvements offered by the tool for commercial edge and cloud AI setups Antmicro builds for its customers.

New (old) approaches to quantization and pruning

The need for size reduction for neural networks dates back to the late eighties when models with around 6000 parameters were considered to be large. To fit the models into extremely limited hardware and reduce the inference time, researchers came up with an optimization algorithm to establish which connections or neurons could be removed with minimal sacrifice of the model’s quality. At that time, papers like Optimal Brain Damage and Optimal Brain Surgeon discussed usage of analytical approaches based on second-order derivatives and Hessians.

These approaches, while too demanding in terms of time and memory complexity, acted as a base for further research, which went towards simpler, approximate techniques, for instance removing connections with the lowest absolute weight value or calculating quantized weights relying on statistics gathered during inference on calibration dataset.

Now these techniques, thanks to technological advances and a need for more accurate and few-shot learning optimizations, are becoming the subject of various papers, optimizations and simplifications for LLM use cases. This research brought to life two algorithms (among others) – GPTQ and SparseGPT.

Both of the above utilize the same mechanism of analyzing second-order derivatives of weights, but introduce novel adjustments to the approach in order to adapt it to large, demanding models. GPTQ iteratively looks for the easiest weights to quantize (the ones that influence the output the least), while SparseGPT looks for the easiest weights to set to zero. Both use second-order derivatives to update the remaining weights to compensate for quality loss resulting from the changes in the current weight, but do it in a batched, per-row manner, allowing to update remaining weights significantly less often. What is more, the usage of the same mechanics allows us to run both quantization and pruning at the same time, speeding the optimization process significantly.

Since both algorithms share the same mechanics for model analysis, combining them and the optimizations they offer is a seamless process.

Combining GPTQ and SparseGPT

To keep track of the newest achievements in LLMs, and put them to good use on edge platforms, we equipped our open source Kenning framework with a reporting capability that provides users with information about LLM performance and quality for QA and summarization tasks. We are also observing the evolution of available optimization algorithms, so we wanted to tap into the benefits coming both from GPTQ and SparseGPT.

Existing runtime implementations tend to focus on just one of the algorithms – usually GPTQ. There are little to no runtime implementations utilizing pruned models with SparseGPT, as leveraging a model’s sparsity is not as straightforward as leveraging their reduced precision. Since GPTQ and SparseGPT use the same tools for model analysis, we implemented a class that combines both algorithms, allowing successful quantization of models to 8 and 4 bits as well as model pruning.

The SparseGPT algorithm implements unstructured pruning, meaning that instead of removing entire neurons or other neural network blocks, it removes individual connections. Without any additional optimizations, or changes to the runtime, unstructured pruning does not provide any improvement to either model size or model performance – it can be used for model compression in storage.

However, SparseGPT allows to enforce patterns into such unstructured pruning where, for example, for matrix rows holding weights for a given layer, for each 4 neighboring weights we can instruct the algorithm to prune only two of these weights. Such a technique is referred to as semi-structured pruning.

Our implementation, adjusted for SparseGPT and GPTQ, is present in the kenning.sparsegpt Python module. The introduced module saves the optimized model in the fast, well-known and flexible Safetensors format. We took the advantage of this flexibility in our integration with our sparse implementation of GEMM in the vLLM runtime, which will be described in the following sections.

With this combined optimization, we can get a quantized and pruned Phi-2 model in around 20 minutes, and larger models, like Mistral 7B take less than an hour.

Elevating semi-structured pruning on Ampere-based NVIDIA GPUs

On the hardware side of the neural network optimizations, NVIDIA is actively extending support for more precisions of weights (BFLOAT16, TF32, FP8, INT4 and INT3) in their Tensor Cores, allowing to compute massive amounts of multiply-add operations on matrices with width and height values equal to usually 8, 16 or 32 in a single instruction (it varies for different value types and GPU architectures, in some cases up to even 128).

With Ampere, NVIDIA introduced sparse matrix multiplication instructions called mma.sp, supporting multiplication of dense tensors by semi-structured tensors. While this requires some additional preparation of data, it results in decently smaller memory usage, and may also introduce a computational improvement, depending on the matrix shape, configuration and the exact hardware architecture.

NVIDIA provides two libraries that utilize mma.sp instructions to perform matrix multiplications – CUSPARSELt and CUTLASS. We selected CUTLASS as it provides full control over the format of matrices and necessary metadata, including their internals, and allows us to run some additional operations (such as dequantization) directly on the compressed matrices.

The family of mma.sp instructions accepts semi-structured matrices following the 2:4 pattern, where 2 out of 4 consecutive values in the matrix have to be zeroed, resulting in a 50% sparsity matrix. Then, all non-zero values from the original matrix are stored densely in a new matrix that is half as wide. Still, we need to hold information about the locations of those non-zero values in the original matrix. For this, we create a new so-called metadata matrix. This metadata matrix has the same dimensionality as the packed matrix, and it holds indices of non-zero values within a 4-element window.

For example, in the first row of the matrix in the animation above, green cells represent non-zero values, and blank cells represent pruned values, then the metadata row will have indices [0,2,0,1,0,3,0,1]. Since there are only 4 possible values of indices (0 to 3), these indices are stored as 2-bit values. Effectively, we packed 16 values from the original matrix (from which half were zeros) into 8 non-zero values and 8 2-bit values. It is worth noting that there is no information loss, only the way in which matrix values are stored has changed.

The packing method results in a substantial memory gain and because the layout of matrices has changed, both disk space and runtime memory requirements are reduced. To draw a picture, let’s consider an example in which a 100x100 4-bit matrix is pruned using a 2:4 pattern and then compressed. The width of the output dense matrix is two times smaller, which makes it 100x50 and the values are still 4-bit. The metadata matrix is of the same size (100x50) but the values are 2-bit. Now, considering the memory, the initial footprint was 40000 bits and after the pruning and compression was performed, the footprint is equal to 100 * 50 * 4 + 100 * 50 * 2 = 30000. In this case, the memory reduction is equal to 25%.

Since we’re introducing new information to the model (metadata matrix) in our kenning.sparsegpt optimizer, it needs to be available during runtime. To do that, we expanded the current .safetensors data layout – each layer now also has a qsparsity_metadata parameter that is a matrix containing the indices of non-zero values. The data type of the matrix is set to 16-bit, so every 8 contiguous values are coalesced and kept as a single value, as described in the NVIDIA ISA documentation.

Implementing a CUDA kernel with sparse matrix support

To tackle aspects such as dequantization of compressed matrices (like handling additional operations around CUSPARSE matrix multiplication), we introduced a CUDA kernel to process data. To track performance of the introduced inference stages, we analyzed the runtime with the NVIDIA Nsight Systems analysis tool.

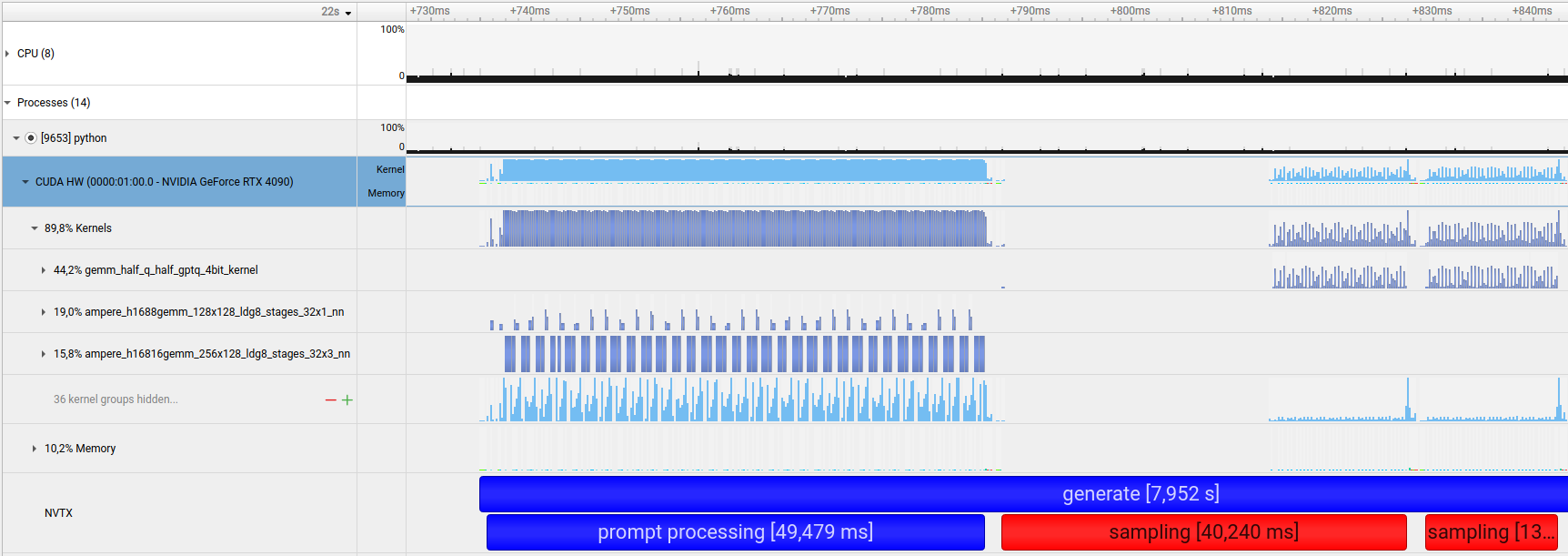Example: An optimized batch consisting of 1 prompt with 512 tokens resulting in 512 tokens produced. Blue represents prompt processing, red represents sampling.

The CUDA kernel operates on compressed and quantized matrices, so it is carefully crafted to produce correct outputs without creating computational overhead. The problem can be easily parallelized, but in order to make it efficient, things like double buffering, or bank conflicts need to be taken into account. Along with the NVIDIA library, the implementation is used to run a full inference process.

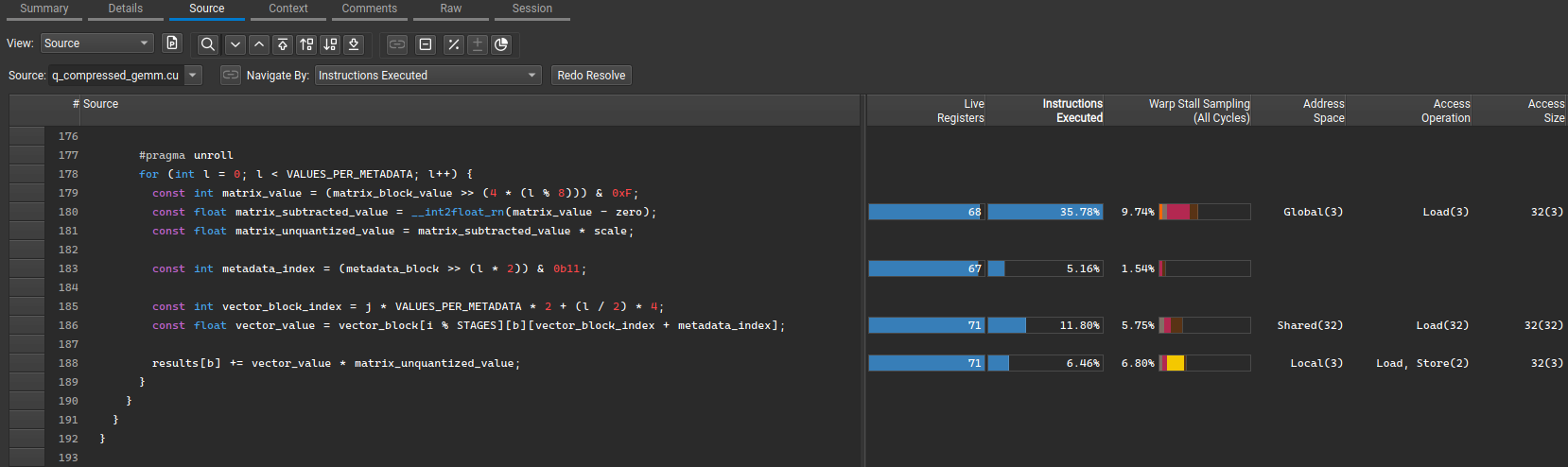Dequantization and decompression stage in our CUDA kernel

Since only one operand in Sparse Tensor Cores can be sparse, we use dense activations, which allow us to skip any further conversions. The link to the kernel can be found in kenning.sparsity_aware_kernel Python module.

Benchmarking the models with Kenning

Optimizing and benchmarking the models was carried out in Antmicro’s Kenning framework. As illustrated in the table above, using just the GPTQ algorithm to quantize the model to 4-bit precision allows us to reduce the size of the Mistral-7B and Phi-2 models by ca. 75%. Pruning brings a further reduction of around 20% of the result.

As for model quality, we can take a look at Rouge scores for the original and optimized model below:

Model quality comparison: native vs. optimized.

Visibly, the quality for Mistral-7B is well-maintained despite pruning and quantization. Obviously, our optimization flow does not take all the credit – the changes in quality metrics also heavily depend on the models used.

As for performance, the current implementation achieves similar inference time to the vLLM runtime for GPTQ-optimized models, so we generally get compressed matrices without sacrificing performance. This results in an over 2.75 faster inference (for batch 1) compared to the native model with token limit equal to 512 on summarization tasks.

The Ampere-based Jetson Orin series ships with RAM capacity ranging from 4 GB to 32 GB. By using these optimizations, larger models can be used on smaller Jetson Orin-based devices like the Jetson Orin Nano without sacrificing inference speeds. In some applications, we have even observed a gain in speed after reducing the size of the models.

Accelerating AI workflows with tailored runtimes

By combining SparseGPT and GPTQ algorithms and implementing a CUDA kernel with sparse matrix support, we were able to equip Kenning with the capability to optimize LLMs to fit into edge AI scenarios utilizing Ampere-based NVIDIA GPUs including the Jetson Orin series, like the low Earth orbit satellite computer we built for Aethero based on our open source Jetson Orin Baseboard.

Antmicro provides comprehensive AI/ML model and runtime optimization services for edge AI applications (computer vision, LLMs, audio processing, etc.) in resource-constrained environments, so that your models can take full advantage of your hardware. We also develop end-to-end edge AI solutions including BSPs along with highly customized hardware. Get in touch at contact@antmicro.com to find out more about how Antmicro’s open source toolkit and expertise can help your business lead in AI innovation and maintain a competitive edge with full ownership of solutions tailored to your use case.